5 min to read

NLP(1) - 언어의 통계학적 접근이란? - 정보량

A Mathematical Theory of Communication 논문 리뷰

Featured image

요즘은 소마에서 하던 프로젝트를 이어하느라, 하루종일 시간을 투자하느라 블로그를 작성할 기회가 많이 없었다.

그런데 요즘 LLM API 자체에 대한 한계를 많이 느끼고, 어떻게 구조를 개선을 하면 좋을 지 고민을 많이했다.

그러나 최신 정보들을 보려고해도 대부분 논문으로 작성된 경우가 많아 현재 지식의 한계를 느끼고, 본질적인 접근을 해야만 더 나은 프로덕트가 나올 수 있을 것 같다는 생각에 미뤄두었던 NLP 공부를 시작해보려한다.

순전히 자신의 공부만을 위해서 정리하다보니, 오개념이 있을 수 있는데 발견되면 친절히 알려주면 좋을 것 같다.

오늘 다룰 개념 - 통계적 접근

AI의 핵심 개념은 통계적 접근이다. 그렇기에 오늘을 언어를 통계적 개념으로 처음 접근한 “C. E. SHANNON”의 “A Mathematical Theory of Communication” 논문에 대해 알아보겠다. (참고로 C는 Claude인데, 우리가 익숙한 AI 서비스 Claude는 이 선생님의 이름에서 따왔다)

1. 정보량이란?

정보량이란 기호 또는 메시지를 선택할 수 있는 전체 경우의 수에 따라 결정되며, 이는 해당 선택이 얼마나 예측 불가능한지를 나타낸다.

그 중 Hartley는 가능한 경우의 수를 로그 함수로 표현하면 정보량을 잘 측정할 수 있다고 보았다. 이 정의는 다음 이유들로 합리적이다.

첫째, 실제로 더 유용하다. 엔지니어링 관점에서 릴레이나 시간 같은 요소를 하나 추가하면 가능한 경우의 수가 두 배가 되는 경우가 많다. 이때 로그의 성질(log₂ ab = log₂ a + log₂ b)을 이용하면, 예컨대 선택지가 하나 추가되면 log₂(기존 경우의 수) + 1 = log₂(새 경우의 수)가 된다.

둘째, 인간의 직관과 일치한다. 예를 들어, 동전 1개보다 2개를 던졌을 때 2배 더 많은 정보를 얻는다는 감각은, 정보량이 2배가 되어야 한다는 직관과 맞닿아 있다.

셋째, 수학적으로 간단하다. 로그는 큰 수의 곱셈을 더하기로 바꿔 계산할 수 있게 해주기 때문에, 경우의 수처럼 커지는 수를 다루기에 유리하다.

여기서, Shannon은 Hartley의 연구에 이어 base를 2로 잡으면 그 단위를 binary digits라고 할 수 있고 더 줄여서 bits라고 할 수 있다고 했고, 참고로 이 단어는 Shannon이 만든게 아니라 다른 수학자인 J. W. Tukey가 먼저 사용했고, Shannon이 널리 퍼뜨렸다.

2. 그래서 이게 왜 중요한건데?

통신에서는 어떤 기호가 도착했다는 것은, 가능한 기호 집합 중 하나가 선택된 결과라고 볼 수 있다.

이 점에 착안하면, 기호이 동일한 확률로 선택되며, 가능한 기호의 총 개수가 일정하다면, 앞서 언급한 로그 함수를 통해 선택된 기호의 정보량을 계산할 수 있다.

예를 들어, 4개의 가능한 경우의 수를 가진 랜덤 뽑기가 있다고 가정해보자.

가능한 기호 집합이 4개라고 할 수 있고, 유저가 그중 하나의 기호를 수신했다고 하면, 이 기호 하나가 전달하는 정보량은 log24 = 2 bits의 정보량을 가진다고 할 수 있다.

여기서 중요한 점은 각각의 정보량은 통계적 의미를 가질 뿐, 의미론적인 값을 가지지는 않는다는 점이다.

즉, 4개의 기호호가 모두 다른 색이거나 내용이 다르더라도, 그중 하나를 받았다는 사실만으로는 2bits의 정보량만을 전달한 것이 된다.

이처럼, Shannon의 논문에서 다룬 정보량의 값이 중요한 이유는, 의미(semantics)와는 무관하게, 오직 확률과 선택지의 수만으로 정보의 양을 객관적으로 측정할 수 있기 때문이다.

3. 이산 채널의 정보량 (1)

모스 부호와 같은 이산 채널의 예시로 정보량을 다뤄보자. 이산 채널이란, 정보가 불연속한 매체를 의미한다.

예를 들어 다음과 같은 기호 선택지가 4개 존재한다고 해보자. [점, 선, 문자 사이 공백, 단어 사이 공백]

각 기호는 같은 확률을 가지고, 1초 동안 보내지며 모든 조합이 가능하다고 가정하면, 이 전신은 얼마나 단위 시간당 정보량을 가질까?

당연히 아래에서 말한 것과 같은 2bits/sec의 정보량을 가진다. (log24 = 2bits, 참고로 bits/sec의 단위는 더 줄여 bps라고 불린다.)

4. 이산 채널의 정보량 (2) - 시간이 다르다면?

그런데 만약, 각각의 기호가 시간이 다르다면? Shannon은 아래와 같이 정의한다.

이산 채널의 용량 ( C )는 다음과 같이 정의된다:

\[C = \lim_{T \to \infty} \frac{\log N(T)}{T}\]

여기서 \( N(T) \)는 시간 \( T \)초 동안 전송할 수 있는 유효한 신호 조합의 수를 의미한다.

모든 기호 조합이 허용되고, 각 기호가 걸리는 시간이 \( t_1, t_2, \ldots, t_n \)이라면,
( N(T) )는 다음과 같은 점화식으로 표현할 수 있다:

\[N(T) = N(T - t_1) + N(T - t_2) + \cdots + N(T - t_n)\]

이 식은 이해하기 어려울 수 있지만, DP(동적 계획법) 문제를 풀 듯이 생각하면 쉽다.
즉, 길이 \( T \)짜리 신호 조합은 마지막에 어떤 기호가 붙었는지에 따라 나뉜다.

예를 들어, 마지막 기호가 \( t_1 \) 길이라면 그 이전까지 만들 수 있었던 경우는 \( N(T \!-\! t_1) \)개이고,
마지막이 \( t_2 \)라면 \( N(T \!-\! t_2) \)개의 조합이 있었을 것이다.
이처럼 가능한 모든 기호에 대해 그 이전 상태의 경우의 수를 합산하면 전체 경우의 수 \( N(T) \)가 구해진다.

근데, 다시 이 식을 보자

\[N(T) = N(T - t_1) + N(T - t_2) + \cdots + N(T - t_n)\]

이 식은 전형적인 선형 점화식으로, 점화식의 해를 지수 함수 꼴로 가정하면 다음과 같이 유도할 수 있다:

\[N(t) \approx X_0^t\]

이를 점화식에 대입하면,

\[X^t = X^{t - t_1} + X^{t - t_2} + \cdots + X^{t - t_n}\]

양변을 \( X^t \)로 나누면,

\[1 = X^{-t_1} + X^{-t_2} + \cdots + X^{-t_n}\]

이 방정식의 가장 큰 실근 \( X_0 \)를 찾고, 앞서 가정한 \( N(T) \approx X_0^T \)를 \( \log N(T) \)에 넣어보면:

\[\log N(T) \approx \log X_0^T = T \log X_0\]

따라서 정보량은:

\[C = \lim_{T \to \infty} \frac{\log N(T)}{T} \approx \lim_{T \to \infty} \frac{T \log X_0}{T} = \log X_0\] \[C = \log_2 X_0\]

즉, 시간당 최대 정보 전송량(채널 용량)은
가능한 신호 수의 지수 성장률 \( X_0 \)에 대한 로그로 계산된다.

5. 이산 채널의 정보량(3) - 모든 조합이 가능하지 않다면?

앞에서 다뤘던 [점, 선, 문자 사이 공백, 단어 사이 공백]의 4가지 신호가 있다고 해보자.

방금 다룬 것처럼 각각의 신호의 시간도 다르고, 이번엔 공백이 연속되면 안 된다는 제약이 붙는다.

이런 경우, 전체 시스템은 아래처럼 두 개의 상태(왼쪽, 오른쪽)를 갖는 그래프로 표현할 수 있다.

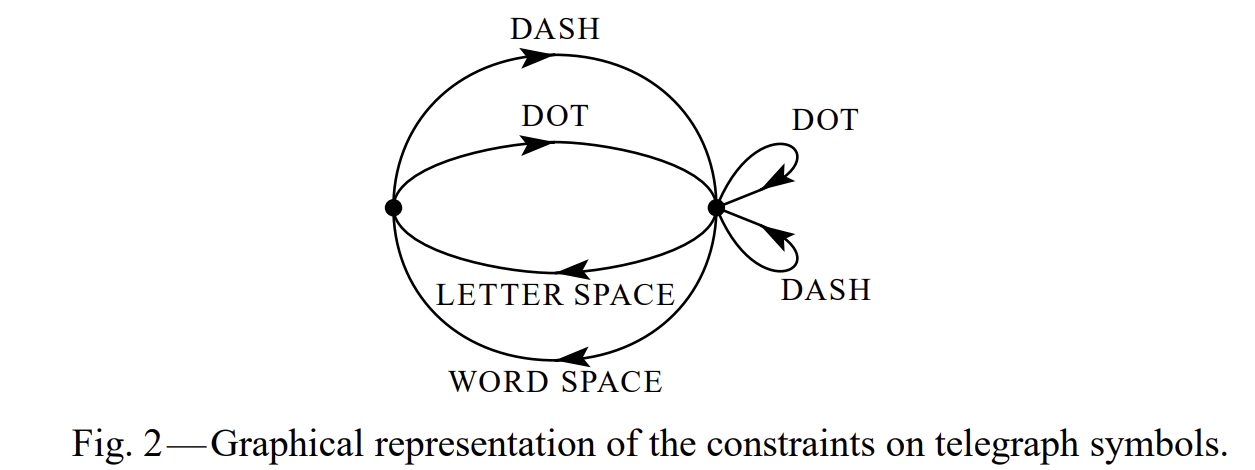
이 시스템에서 상태는 다음처럼 정의된다:

A 상태 (공백은 B → A만 가능)

\[N_\text{A}(T) = N_\text{B}(T - T_\text{LETTER}) + N_\text{B}(T - T_\text{WORD})\]

B 상태 (DOT, DASH는 어디서든 가능)

\[N_\text{B}(T) = N_\text{A}(T - T_\text{DOT}) + N_\text{A}(T - T_\text{DASH}) + N_\text{B}(T - T_\text{DOT}) + N_\text{B}(T - T_\text{DASH})\]

즉, 이 두 식을 해결하는 W를 구하는 것이 문제이고, 아래의 식을 풀기 위해 행렬을 도입한다.

\[N_\text{A}(T) = \alpha_\text{A} W^T,\quad N_\text{B}(T) = \alpha_\text{B} W^T\] \[\begin{bmatrix} \alpha_\text{A} \\ \alpha_\text{B} \end{bmatrix} = \begin{bmatrix} 0 & W^{-T_\text{LETTER}} + W^{-T_\text{WORD}} \\ W^{-T_\text{DOT}} + W^{-T_\text{DASH}} & W^{-T_\text{DOT}} + W^{-T_\text{DASH}} \end{bmatrix} \begin{bmatrix} \alpha_\text{A} \\ \alpha_\text{B} \end{bmatrix}\] \[\left| \begin{array}{cc} -1 & W^{-T_\text{LETTER}} + W^{-T_\text{WORD}} \\ W^{-T_\text{DOT}} + W^{-T_\text{DASH}} & W^{-T_\text{DOT}} + W^{-T_\text{DASH}} - 1 \end{array} \right| = 0\] \[1 = (W^{-T_\text{LETTER}} + W^{-T_\text{WORD}})(W^{-T_\text{DOT}} + W^{-T_\text{DASH}}) + (W^{-T_\text{DOT}} + W^{-T_\text{DASH}})\]

이 방정식을 만족하는 가장 큰 실수 해 \( W_0 \)를 구하면,

\[C = \log_2 W_0\]

이게 바로 제약이 있는 이산 채널의 최대 정보량이 된다.

다음 시간에는 이 정보량과 함께, 섀넌의 n-gram 모델에 대해 계속 살펴보겠다.