13 min to read
NLP(5) - McCulloch와 pitts의 M-P모델이란?
A Logical Calculus Of The Ideas Immanent In Nervous Activity 논문 리뷰
저번 Bengio의 논문 도입부에서 너무 많은 어려운 정보가 나와 선행 지식을 챙겨가며 공부하는 것으로 결정했다.
우선 신경망(Neural Network)라는 단어가 자주 나오는데, 이 신경망을 이해하기 위해서 가장 기초적인 모델인 M-P모델이라는 모델부터 공부를 해보도록 한다.
1. 뉴런 모델의 도입 배경
좀 뜬금없지만, 앞으로 나오게 될 NLP 모델을 이해하기 위해서는 이 배경을 알아두면 좋다.
사실 인공지능이라는 개념은 컴퓨터 과학에서 연구하던 과정에서 나온 것이 아니라, 뇌의 인지 과정을 이해하던 중에 처음 나오게 되었다.
1940년대 신경과학자들은 뇌의 인지 과정을 두 가지 방향에서 접근했다.
하나는 “기호주의”로, 뇌는 규칙 기반의 논리적 연산을 통해서 작동한다는 관점이고, 다른 하나는 “연결주의”로, 규칙 기반이 아니라 수많은 기본 단위(뉴런)들이 연결된 채 만들어 내는 경험을 통해 작동한다는 관점이다.
이 두 관점을 이해하기 위해서는 공통적으로 “뉴런”이라는 것을 이해할 필요가 있다.
2. 뉴런이란?
인간의 뇌 속, 가장 작은 단위는 “뉴런”이라는 것으로 구성되어있다.
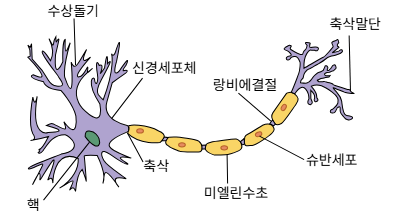
뉴런은 다음과 같은 방식으로 작동했다.
-
수상돌기(dendrite)를 통해 다른 뉴런으로부터 전기적 자극을 받는다.
-
신경세포체(soma)에서 이 자극의 총합이 임계값(threshold)을 넘으면, 축삭(axon)을 통해 다음 뉴런으로 전기 신호를 전달한다.
-
임계값을 넘지 못하면 신호는 전달되지 않는다.
그런데 이거 완전 if-else 문과 비슷하지 않은가?
이런 점에 주목한 McCulloch는 뇌의 가장 작은 단위인 뉴런을 논리적인 연산 단위로 모델링할 수 있다고 보았고, 결국 뇌 전체도 수많은 논리적 뉴런들로 구성된 계산 가능한 네트워크라고 생각했다.
즉, 기호주의의 관점에서 최초로 인간의 신경 세포인 뉴런을 논리적으로 모델링한 시도를 하게 된다.
3. McCulloch와 Pitts의 M-P모델이란?
McCulloch와 Pitts는 뇌의 생물학적 사실을 기반으로 다음과 같은 가정을 가진 M-P모델을 만들어 낸다. (아래부터는 McCullouch만 표기함.)
-
뉴런의 활동은 전부 아니면 전무(all-or-none) 방식으로 발생한다.
-
뉴런이 흥분되기 위해서는 정해진 수의 시냅스가 잠복 통합 시간(latent addition period) 내에 자극을 받아야 하며, 이 수는 이전 활동이나 자극 위치와 무관하다.
-
신경계 내에서 중요한 시간 지연은 시냅스 지연뿐이다.
-
억제 시냅스가 작동하는 순간에는 해당 뉴런은 절대적으로 흥분할 수 없다.
-
신경망의 구조는 시간이 지나도 변하지 않는다.
참고로, 여기서 시냅스란 다른 뉴런과의 연결을 의미한다. 신경망(Neural Network)은 뉴런(노드)들이 시냅스(연결선)를 통해 연결되어 이루어진 계산 구조 또는 시스템을 말한다. 이 M-P모델에서 중요한 점은 모든 것을 논리적으로 표현할 수 있다는 것이다. 원문은 모두 수학적 표기로 되어있지만, 우리는 수학보다는 코드가 가까운 프로그래머이니까 각 뉴런의 활동을 코드로 만들어보자!
4. M-P모델 구현
우선 1번 가정에서 말한 “전부 아니면 전무(all-or-none)” 원리는, 뉴런의 상태가 True 또는 False 중 하나로만 표현된다는 의미다. 따라서 Boolean 값으로 모델링할 수 있다. 다음은 뉴런 클래스를 정의한 예시다.
우리는 근사한 코드를 짜는 것보다, 논리를 이해하는 게 우선이기에 getter나 setter는 생략하겠다.
class Neuron:
#Constructor
def __init__(self, value):
self.value : bool = value
2번 가정에 따르면, 뉴런은 신호를 주고받을 수 있어야 하며, 잠복 통합 시간(latent period) 동안 일정 임계값(threshold) 이상의 신호가 입력되었을 때만 발화한다.
따라서 뉴런에는 신호를 주고받는 기능과 더불어, 임계값과 잠복 시간을 속성으로 포함해야 한다.
아래는 이를 반영한 구현이다:
import asyncio # 비동기 작업이 필요하니까
class Neuron:
#Constructor
def __init__(self, value=False, threshold=3, latent_period=5):
self.value = value
self.threshold = threshold
self.latent_period = latent_period
self.got_signal = 0
self.recieve_status = False
# 다른 뉴런에게 쏘기
def send_signal(self, other_neuron):
if self.value and other_neuron.recieve_status:
other_neuron.got_signal += 1
# 비동기적으로 켜야, 다른 뉴런에게 특정 시간 동안만 받을 수 있음.
async def receive_signal(self):
self.recieve_status = True
await asyncio.sleep(self.latent_period)
self.recieve_status = False
self.value = self.got_signal >= self.threshold
print(f"I got {self.got_signal} signals!")
print(f"So, I am {self.value} now!")
self.got_signal = 0
import random
# 상위 함수니까 비동기 필요
async def main():
neurons = []
target_neuron = Neuron(False, threshold=3, latent_period=3)
for _ in range(5):
# T/F 두 가지 값만 가지니까
neuron = Neuron(value=bool(random.getrandbits(1)))
print(f"Neuron created with value: {neuron.value}")
neurons.append(neuron)
# target 뉴런이 신호를 받을 준비
receive_task = asyncio.create_task(target_neuron.receive_signal())
# 잠깐 기다렸다가 신호 보냄
await asyncio.sleep(1)
for neuron in neurons:
neuron.send_signal(target_neuron)
await receive_task
이렇게 하면 M-P모델과 비슷하게 2번 정리까지 모델링을 따라할 수 있다.
랜덤으로 뉴런들의 값에 따라 어떻게 값이 나오는지 확인해보자 (사실 비동기를 제외하면 초보 파이썬 실습과도 비슷하다)
Neuron created with value: True
Neuron created with value: True
Neuron created with value: True
Neuron created with value: False
Neuron created with value: True
I got 4 signals!
So, I am True now!
Neuron created with value: False
Neuron created with value: True
Neuron created with value: False
Neuron created with value: True
Neuron created with value: False
I got 2 signals!
So, I am False now!
이제 3번 정리를 따라가보자. 시냅스 지연이라는 표현이 있는데, 이는 쉽게 말하면 지금처럼 Value가 true라고 즉시 다른 뉴런에 쏠 수 있는 것이 아니라 특정 시간이 쏘는데 필요하다는 뜻이다.
즉, 시냅스가 쏘는 것도 동기적으로 구현이 아니라 비동기로 구현하면 된다!
def __init__(self, delay, value=False, threshold=3, latent_period=5):
self.value: bool = value
self.threshold: int = threshold
self.latent_period: int = latent_period
self.got_signal: int = 0
self.recieve_status: bool = False
self.delay: int = delay # delay 추가
# 비동기화
async def send_signal(self, other_neuron):
await asyncio.sleep(self.delay)
if self.value and other_neuron.recieve_status:
other_neuron.got_signal += 1
async def main():
neurons = []
target_neuron = Neuron(False, threshold=3, latent_period=3)
for _ in range(5):
neuron = Neuron(value=bool(random.getrandbits(1)), delay = random.randint(1, 6))
print(f"Neuron created with value: {neuron.value}, delay: {neuron.delay}")
neurons.append(neuron)
# 비동기화
tasks = [asyncio.create_task(neuron.send_signal(target_neuron)) for neuron in neurons]
tasks.append(asyncio.create_task(target_neuron.receive_signal()))
await asyncio.gather(*tasks)
결과는 이렇게 됨을 알 수 있다.
# threshold는 5
Neuron created with value: True, delay: 3
Neuron created with value: False, delay: 2
Neuron created with value: True, delay: 2
Neuron created with value: True, delay: 6 (시간 넘어서 out)
Neuron created with value: False, delay: 4
I got 2 signals!
So, I am False now!
Neuron created with value: True, delay: 3
Neuron created with value: True, delay: 6 (시간 넘어서 out)
Neuron created with value: True, delay: 3
Neuron created with value: True, delay: 2
Neuron created with value: False, delay: 4
I got 3 signals!
So, I am True now!
거의 다 왔다. 이제 4번 억제 시냅스를 구현해보자.
받는 쪽 뉴런의 흥분 조건이 충족되더라도, 억제 시냅스를 통해 들어온 신호가 있다면 발화하지 않는다.
즉, 뉴런의 성질 중 억제의 기능이 있냐, 없냐를 속성으로 구현해주면 되고 조건문을 통해 단 하나의 억제 시냅스라도 on이 되는 경우 false를 반환하면 된다.
import asyncio
class Neuron:
def __init__(self, delay, value=False, threshold=3, latent_period=5, inhibitory=False):
self.value: bool = value
self.threshold: int = threshold
self.latent_period: int = latent_period
self.got_signal: int = 0
# 억제 시냅스에게 신호를 받았는가?
self.got_inhibitory: bool = False
self.recieve_status: bool = False
self.delay: int = delay
# 뉴런이 억제의 성질을 가지는가?
self.inhibitory = inhibitory
async def send_signal(self, other_neuron):
await asyncio.sleep(self.delay)
if self.value and other_neuron.recieve_status:
other_neuron.got_signal += 1
if self.inhibitory:
# 억제 시냅스를 하나라도 받으면 False니까
other_neuron.got_inhibitory = True
async def receive_signal(self):
self.recieve_status = True
self.recieve_status = False
# 억제 시냅스를 하나라도 받았다면?
if self.got_inhibitory:
self.value = False
print(f"I got {self.got_signal} signals!")
print(f"But I got inhibitory signals!")
print(f"So, I am {self.value} now!")
self.got_signal = 0
self.got_inhibitory = False
return
self.value = self.got_signal >= self.threshold
print(f"I got {self.got_signal} signals!")
print(f"So, I am {self.value} now!")
self.got_signal = 0
import random
async def main():
neurons = []
target_neuron = Neuron(False, threshold=3, latent_period=5)
for _ in range(5):
neuron = Neuron(value=bool(random.getrandbits(1)), delay = random.randint(1, 6), inhibitory=random.choices([True, False], weights=[1, 9])[0])
print(f"Neuron created with value: {neuron.value}, delay: {neuron.delay}, inhibitory: {neuron.inhibitory}")
neurons.append(neuron)
tasks = [asyncio.create_task(neuron.send_signal(target_neuron)) for neuron in neurons]
tasks.append(asyncio.create_task(target_neuron.receive_signal()))
await asyncio.gather(*tasks)
다음과 같은 결과를 받을 수 있다!
Neuron created with value: True, delay: 4, inhibitory: False
Neuron created with value: False, delay: 5, inhibitory: False
Neuron created with value: False, delay: 3, inhibitory: True
Neuron created with value: True, delay: 1, inhibitory: False
Neuron created with value: True, delay: 2, inhibitory: False
I got 3 signals!
So, I am True now!
Neuron created with value: False, delay: 4, inhibitory: True
Neuron created with value: True, delay: 4, inhibitory: False
Neuron created with value: True, delay: 2, inhibitory: False
Neuron created with value: True, delay: 5, inhibitory: True
Neuron created with value: True, delay: 3, inhibitory: False
I got 4 signals!
But I got inhibitory signals!
So, I am False now!
5. M-P모델의 의의와 한계
지금까지 M-P모델을 1번부터 4번까지 하나씩 따라가며 구현해보았다.
여기서 우리는 뇌의 작동 원리를 수학이나 기호가 아닌, 단순한 불리언 연산으로 추상화할 수 있다는 점을 알 수 있었다.
이 모델이 가지는 가장 큰 의의는, 뉴런을 논리적 단위로 바라본 최초의 시도라는 점이다.
이전까지는 뇌가 너무 복잡해서 수학적으로 다룰 수 없다고 여겨졌지만, McCulloch는 “복잡해 보이는 사고도 사실은 단순한 논리 연산의 조합일 수 있다”는 가능성을 열었다.
또한, 지금 우리가 배울 수 있는 신경망, 퍼셉트론, 딥러닝 같은 개념들도 사실은 여기서 시작된 셈이다.
아이러니하게도, 기호주의적 관점에서 정의된 M-P모델이 이후 연결주의의 대표 모델인 퍼셉트론의 기반이 되었다.
하지만 당연히 한계도 있다.
-
학습이라는 개념이 없다. 한 번 만들어진 신경망은 계속 고정되어 있고, 연결이나 임계값은 바뀌지 않는다. (5번 가정 때문)
-
모든 뉴런이 동일한 구조를 가진다. 생물학적으로 다양한 뉴런의 특성을 무시하고, 지나치게 단순화되어 있다.
-
0 또는 1로만 작동한다. 확률적 판단이나 연속적인 값 계산이 불가능하다.
-
XOR, NOR 같은 비선형 논리 연산을 표현할 수 없다. 음수 가중치나 학습이 불가능하기 때문에, 특정 논리 구조는 M-P 모델로 구현 자체가 되지 않는다
결국 이 모델은, 뇌를 완벽하게 모사하려는 게 아니라, 뇌도 계산 가능한 구조일 수 있다는 아이디어를 실험적으로 보여준 것에 가깝다.
이제 우리는 이 기반을 가지고 다음 시간에는 연결주의의 기본, 퍼셉트론 모델을 통해 신경망에 대해서 알아보겠다.

Comments