5 min to read
NLP(6) - Rosenblatt의 Perceptron 모델이란?
The Perceptron, A Probabilistic Model For Information Storage And Organization In The Brain 논문 리뷰
우리는 지금까지, N-gram 이후의 다음 모델인 Bengio의 신경 확률적 언어 모델을 공부하기 위해 선행 지식을 공부하고 있다.
저번 시간은 McCulluch와 Pitts의 M-P 모델을 배웠는데, 최초로 인간의 뇌를 기호적으로 모델링했다는 점에서 의의를 가졌다.
그러나, 다소 한계가 명확했는데, 다음과 같았다.
-
학습이라는 개념이 없다. 한 번 만들어진 신경망은 계속 고정되어 있고, 연결이나 임계값은 바뀌지 않는다. (5번 가정 때문)
-
모든 뉴런이 동일한 구조를 가진다. 생물학적으로 다양한 뉴런의 특성을 무시하고, 지나치게 단순화되어 있다.
-
0 또는 1로만 작동한다. 확률적 판단이나 연속적인 값 계산이 불가능하다.
-
XOR, NOR 같은 비선형 논리 연산을 표현할 수 없다. 음수 가중치나 학습이 불가능하기 때문에, 특정 논리 구조는 M-P 모델로 구현 자체가 되지 않는다
이처럼 한계가 명확했던 M-P 모델은, 이후 뇌과학과 인공지능 연구가 기호주의에서 연결주의로 넘어가는 계기가 되었다.
1. 퍼셉트론 모델의 등장
연결주의자였던 Rosenblatt은 M-P 모델의 5번 가정, 신경망의 구조는 고정되어 있다는 주장을 정면으로 반박한다.
그는 뇌의 학습 과정을 설명하기 위해, 연결이 고정된 논리적 모델이 아닌, 확률적 초기화와 학습에 따른 변화가 가능한 퍼셉트론 모델을 제안한다.
2. Rosenblatt의 퍼셉트론 모델의 주요 가정
퍼셉트론 모델의 주요 가정은 다음과 같이 시작한다.
-
학습과 인식에 관여하는 신경계의 물리적 연결은 개체마다 동일하지 않다.
-
중요한 신경망은 태어날 때부터 대부분 무작위로 구성되어 있으며, 일부 유전적 제약만을 따른다.
-
초기 연결 구조는 가소성(plasticity)을 가지며, 뉴런이 활성화된 후에는 연결될 확률이 변화한다.
-
강화(positive/negative reinforcement)**는 연결 형성 과정을 도와주거나 방해할 수 있다.
-
이 시스템에서 유사성(similarity)이란, 비슷한 자극이 같은 뉴런 집합을 활성화하는 경향으로 나타나며, 이 구조는 환경과의 상호작용을 통해 발달한다.
3번 가정부터 보면, M-P 모델과는 달리 뉴런과 뉴런을 연결하는 시냅스는 확률적으로 연결된다.
즉, 모든 연결이 정해진 게 아니라 처음부터 랜덤하게 연결된 상태에서 시작한다는 거다.
그리고 4번 가정은, 그 연결 확률이 “강화”라는 과정 속에서 변한다는 걸 말한다. 어떤 자극이 반복되거나, 보상이 주어지면 그 연결은 점점 강해지고, 반대로 잘못된 연결은 약해진다.
5번에서는 이 과정을 통해 비슷한 자극이 자주 같은 뉴런과 시냅스를 활성화시키게 되고, 이게 반복되면 그 경로가 점점 굳어진다. 우리는 이런 걸 자연스럽게 “학습”이라고 부른다.
3. 퍼셉트론 모델 구성
퍼셉트론 모델은 감각 뉴런에서 오는 자극(S-unit), 중간에서 내부적으로 처리하는 뉴런(A-unit), 최종적으로 판단을 내리는 뉴런(R-unit)으로 나뉘어진다.
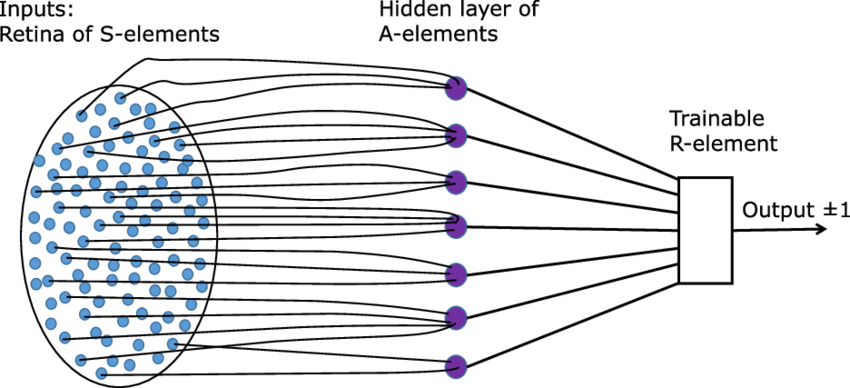
M-P 모델과 달리, 퍼셉트론에서는 각 유닛들의 시냅스가 “강화” 또는 “억제”되는 방향으로 가중치가 조정될 수 있다.
그리고 R-unit이 정답 반응을 했을 때, 그 정답 반응에 기여한 A-unit들과의 연결은 강화되고, 오답이었다면 잘못된 연결은 억제(감소)된다.
즉, 퍼셉트론은 피드백에 따라 연결 강도를 조정하는 학습 시스템이다.
4. 퍼셉트론의 수학적 배경
퍼셉트론 모델은 S‑unit → A‑unit → R‑unit 구조다.
M‑P 모델과 달리 시냅스 가중치가 강화/억제 방향으로 학습에 따라 달라진다.
R‑unit이 정답이면 관련 A‑unit 연결은 강화되고, 오답이면 억제된다.
A‑unit 발화 확률 \(P_a\)은 다음과 같이 구할 수 있다.
\[P_a \;=\; \sum_{e=0}^{\infty} \sum_{i=0}^{e-\theta} P(e,i)\] \[P(e,i) =\binom{x}{e} E^{e}(1-E)^{x-e}\; \binom{y}{i} I^{i}(1-I)^{y-i}\]- \(e\): 흥분성 시냅스 수
- \(i\): 억제성 시냅스 수
- \(\theta\): 임계값
조금 복잡해 보이지만, 흥분성 시냅스 수와 억제성 시냅스 수의 차이가 임계값보다 많은 모든 조합에 대한 확률을 더한 값이다.
다음은 \(S_1\)의 상태 이후, \(S_2\) 상태가 일어날 조건부 확률이다.
\[P_c =\! \sum_{e,i,l_e,l_i,g_e,g_i} P(e,i,l_e,l_i,g_e,g_i), \quad e-i-l_i+l_e+g_e-g_i\ge\theta\] \[\begin{aligned} P(e,i,l_e,l_i,g_e,g_i)= {} & \binom{x}{e}E^{e}(1-E)^{x-e} \binom{y}{i}I^{i}(1-I)^{y-i} \\[6pt] & \binom{e}{l_e}L^{l_e}(1-L)^{e-l_e} \binom{i}{l_i}L^{l_i}(1-L)^{i-l_i} \\[6pt] & \binom{x-e}{g_e}G^{g_e}(1-G)^{x-e-g_e} \binom{y-i}{g_i}G^{g_i}(1-G)^{y-i-g_i} \end{aligned}\]| 기호 | 뜻 |
|---|---|
| \(x,y\) | A‑unit 에 달린 전체 흥분 / 억제 시냅스 수 |
| \(e,i\) | \(S_1\) 자극에서 실제로 켜진 흥분 / 억제 시냅스 수 |
| \(l_e,l_i\) | \(S_1→S_2\) 사이에 사라진 흥분 / 억제 시냅스 수 |
| \(g_e,g_i\) | \(S_2\) 에서 새로 켜진 흥분 / 억제 시냅스 수 |
| \(E,I\) | 흥분·억제 시냅스 하나가 \(S_1\) 때 켜질 확률 |
| \(L\) | \(S_1\) 전용 영역( lost ) 비율 |
| \(G\) | \(S_2\) 전용 영역( gained ) 비율 |
| \(\theta\) | A‑unit 임계값 |
이 역시 복잡해보이지만, 다음과 같다.
- 먼저 \(S_1\) 에서 A‑unit 이 발화할 확률 → \(P_a\)
- 그 뒤 \(S_1→S_2\) 로 갈 때 시냅스가 사라지거나( \(L\) ) / 새로 생기거나( \(G\) ) 하는 경우를 전부 곱셈
- 새로 계산된 순흥분이 임계값을 넘으면 \(S_2\) 에서도 발화
- 모든 가능성을 더한 값이 바로 \(P_c\)
결국 \(P_c = P_a \times (\text{변화 확률}) \times (\text{임계 조건})\)의 누적합 구조다.
마지막으로, R-unit이 정답을 선택할 확률 \(P_r\)이다.
각 A에서 오는 모든 확률을 모든 발화를 독립 사건으로 가정하고 조합을 계산하여, 표준 분포로 근사한다.
그럼 아래와 같은 식으로 일반화 할 수 있는데, \(R_i\)가 정답, \(R_j\)가 오답인 상황에서 \(P_r\) 다음과 같이 나타낼 수 있다.
\[P_r\!\bigl(R_i > R_j \;\vert\; S_t\bigr) \;=\; \bigl[\,1-(1-P_a)^{N_e^{(i)}}\bigr]\; \Phi\!\bigl(Z_{ij}\bigr)\]| 기호 | 정의 |
|---|---|
| \(R_i,\,R_j\) | 비교 대상 두 반응(response) 뉴런 |
| \(S_t\) | 현재 테스트 자극 |
| \(N_{ar}^{(i)}\) | 자극 \(S_t\) 에 대해 \(R_i\) 소스‑셋 중 실제로 발화한 A‑unit 개수 |
| \(N_e^{(i)}\) | \(R_i\) 에만 연결되고 \(R_j\) 와는 공유되지 않는 “효과적 A‑unit” 개수 |
| \(\Phi(\cdot)\) | 표준 정규 누적분포함수 (CDF) |
| \(Z_{ij}\) | 두 반응 세트의 평균‑차/합 분산 정규화 점수 \(\displaystyle Z_{ij}= \frac{c_1\,n_{sr}+c_2}{\sqrt{c_3\,n_{sr}+c_4}}\) — 논문에서 경험적·조합적으로 얻은 계수 \({c_k}\) 적용 |
즉, 정답 시 유효한 A-unit 중 단 하나도 켜지지 않을 확률을 1에서 뺀 확률에 정답 세트와 오답 세트의 확률 차를 곱해서 계산해주면 된다.
5. 퍼셉트론의 의의와 한계
퍼셉트론 모델은 최초로 ‘학습 가능한 신경망’을 제안했다는 점에서 큰 의의가 있다. M-P 모델이 고정된 구조였다면, 퍼셉트론은 자극과 보상에 따라 시냅스의 연결 강도를 조절하며, 기계가 스스로 학습할 수 있다는 가능성을 처음으로 보여주었다.
또한, 뉴런 단위의 계산이 논리 연산처럼 구현될 수 있다는 점에서, 인간의 인지 과정을 수학적으로 모델링한 최초의 연결주의적 시도이기도 하다. 이후 등장하는 신경망 구조들은 대부분 퍼셉트론의 기본 구조(S → A → R)와 학습 개념을 확장한 형태로 발전하게 된다.
하지만 퍼셉트론은 여러 가지 한계를 지녔다.
- 단층 퍼셉트론으로는 XOR처럼 선형적으로 분리되지 않는 문제를 해결할 수 없다.
- 학습 방식이 자극과 정답에 대한 강화·억제 규칙만으로 구성되어 있어, 복잡한 패턴을 유연하게 학습하는 데 한계가 있었다.
하지만 무엇보다도 중요한 한계는, 퍼셉트론에서는 가중치를 바꾸는 행위 자체를 외부가 직접 해줘야 한다는 점이다. 정답을 알고 있는 ‘지도자’가 “이건 맞았으니 연결을 강화해”처럼 학습 규칙을 외부에서 지시하고 실행해줘야만 가중치가 바뀐다. 즉, 퍼셉트론은 학습 규칙이 모델 안에 내재되어 있지 않고, 외부의 개입 없이는 변화할 수 없는 수동적인 구조다.
다음 시간은 퍼셉트론을 직접 구현해서 실습해보는 시간을 가지겠다.

Comments