14 min to read
자료구조(18) - 최소 스패닝 트리
최소 스패닝 트리

🔚 짧게 하는 복습
✅ 1. 서로소 집합(유니온 파인드) 정의를 안다.
✅ 2. 서로소 집합(유니온 파인드)의 ADT를 구현할 수 있다.
✅ 3. 경로 압축을 통해서 서로소 집합(유니온 파인드)의 ADT를 구할 수 있다.
혹시 기억이 안 난다면, 다시 돌아가자
이제 그래프의 마지막 강의로 스패닝 트리를 다룰 시간이다. (물론 이게 그래프의 전부는 아니다.)
혹시 그래프 첫 시간에 다루었던 내용인데, 트리는 어떤 종류의 특별한 그래프라고 했었는지 기억하는가?
트리란 연결, 비순환, 무향 그래프라고 했다. 그렇기에 모든 트리는 그래프라고 했다.
이번 시간은 그래프를 마무리하며, 트리와 그래프 두 개념을 연결하는 스패닝 트리에 대해 다루어 볼 것이다.
스패닝 트리란?
스패닝 트리란 그래프 내의 모든 정점을 포함하면서, 그래프의 모든 간선을 사용해 얻을 수 있는 트리이다.
또한, 그래프의 연결성을 유지하면서 사이클을 포함하지 않는 것이 핵심이다.
아래의 그래프로 예를 들어 보겠다.
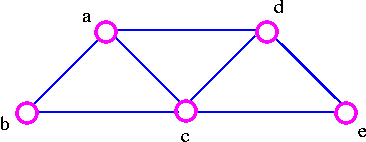
연결성을 유지하면서, 사이클을 포함하지 않는다면 아래와 같은 스패닝 트리를 만들 수 있다.
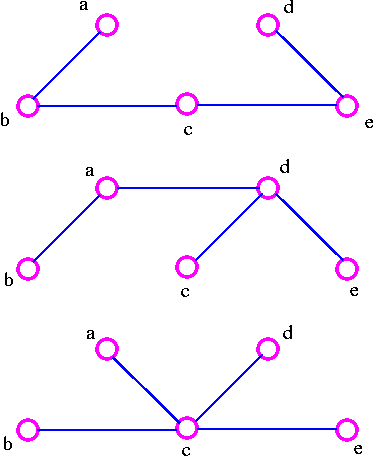
(물론, 다른 스패닝 트리도 만들 수 있다.)
최소 스패닝 트리란?
스패닝 트리는 모든 정점의 연결성을 보장해야 할 때, 주로 사용된다.
그런데 현실적인 문제에서는 사실 비가중치 그래프가 아니라 가중치 그래프인 상황이 많이 나타난다.
네트워크의 공유기 연결이나 마을의 전선 배치 등의 문제에서 모든 정점에 연결하고 싶은데, 그뿐 아니라 비용까지 가장 적기를 바라는 상황이 발생한다.
당연히 거리가 멀어질수록, 더 큰 비용이 들 것이다.
이를 그래프로 표현하면 네트워크의 공유기와 공유기 혹은 마을의 가구와 가구 사이 거리를 가중치로 나타낼 수 있다.
그리고 우리의 목표는 이 그래프에서 가중치 합이 가장 작은 스패닝 트리를 구하면 되는 것이다.
가중치 합이 가장 작은 스패닝 트리를 최소 스패닝 트리(Minimum Spanning Tree)라고 한다.
아래의 그래프를 예를 들어보자.
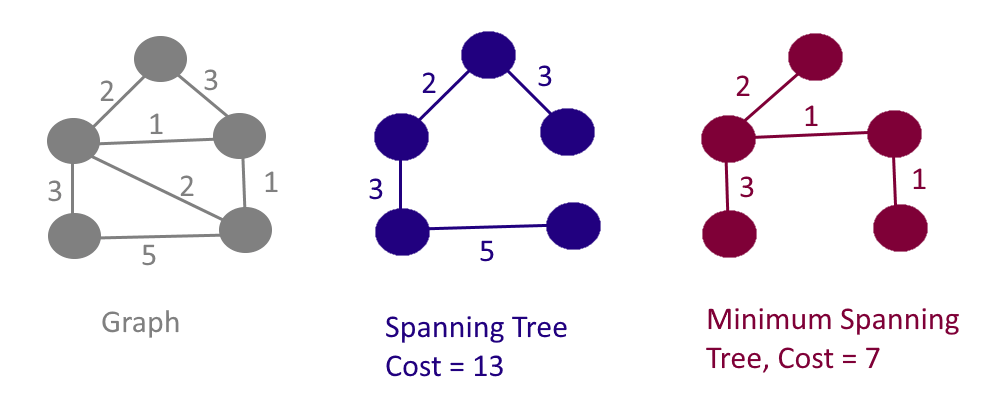
여러 스패닝 트리가 있지만, 가장 오른쪽의 스패닝 트리가 가중치 합이 7로 최소 스패닝 트리(Minimum Spanning Tree)가 된다. (궁금하면 직접 해보자!)
그렇다면 이제부터는 그래프를 입력받았을 때, 최소 스패닝 트리를 구하는 알고리즘에 대해 알아보자.
크게 두 가지 방법으로 나뉘는데, 크루스칼 알고리즘과 프림 알고리즘이다.
크루스칼 알고리즘
우선은 조금 당황스럽겠지만, 알고리즘의 증명은 모두 읽어볼 거리로 넘기겠다.
증명하려면 수학적 지식부터 다루어야 하는데, 그렇게 하면 주객전도가 될 것 같다.
크루스칼 알고리즘은 아래의 동작으로 정의된다.
-
간선들을 가중치의 오름차순으로 정렬한다.
-
정렬된 간선 리스트에서 순서대로 간선을 선택하면서, 해당 간선을 추가했을 때 사이클이 형성되지 않는지 확인한다.
-
사이클이 형성되지 않으면 해당 간선을 최소 스패닝 트리에 추가한다.
-
모든 정점이 포함될 때까지 반복한다.
핵심 키워드를 뽑자면, 정렬, 사이클, 포함이다.
정렬하면 여러 방법이 있지만, 이번에는 복습을 위해 힙을 이용해 구현하는 우선순위 큐(Priority Queue)를 쓸 것이다.
사이클과 포함 관계는 어떻게 파악해야 할까? 사실 둘은 똑같은 질문이다.
연결된 집합/ 아직 연결되지 않은 집합 2개로 분류해서 원소가 어디 속해있는지 확인하면 되기 때문이다.
그러면 원소는 두 집합에 동시에 존재할 수 없다. 무슨 집합…? 바로 서로소 집합(유니온 파인드)이다.
조금 복잡하지만, 천천히 따라와 보자.
Heap 코드가 필요하다면? (구조체 Min 힙으로 수정이 필요함)
#include <stdio.h>
#include <stdlib.h>
#include "Heap.h"
#include "Union_find.h"
int Kruskal(info info_arr[], const int arr_num) {
Heap st = NULL;
int num_of_nodes = 0;
// 미리 만든 힙 이용
int arr[NODE + 1] = { 0 , };
init(arr);
// 미리 만든 유니온 파인드 사용
for (int i = 0; i < arr_num; i++) {
insert(&st, info_arr[i], &num_of_nodes);
} // 힙에 넣어서 하나씩 pop해서 사용
int total_cost = 0; // 총 가중치 합
for (int i = 0; i < arr_num; i++) {
info* temp= Delete(&st, &num_of_nodes);
// 정렬된 간선 리스트에서 순서대로 간선을 선택하면서
if (find(arr, temp->vertex1) != find(arr, temp->vertex2)) {
_union(arr, temp->vertex1, temp->vertex2);
//한 집합으로 연결
total_cost += temp->weight;
// 가중치를 더함
printf("total_cost : %d\n\n", total_cost);
}
else {
continue;// 아닐시 패스
}
}
return total_cost;
}
int main(void) {
info arr[] = { {1, 2, 2}, {1, 3, 3}, {2, 3, 1}, {2, 4, 3}, {2, 5, 2}, {4, 5, 5}, {3, 5, 1}};
// 정점 연결, 가중치 정보
int arr_num = sizeof(arr) / sizeof(info);
printf("The minimum cost of spanning tree is %d", Kruskal(arr, arr_num));
}
위 코드는 아래의 이미지를 좌측 상단에서 우측 하단으로 번호를 매겨 최소 스패닝 트리를 구하는 코드이다.

결과창
2 and 3 is merged
total_cost : 1
3 and 5 is merged
total_cost : 2
1 and 2 is merged
total_cost : 4
2 and 4 is merged
total_cost : 7
The minimum cost of spanning tree is 7
그림대로 (1,2), (2,3), (2, 4), (3, 5)를 연결해 총 7이 됨을 알 수 있다.
프림 알고리즘
프림 알고리즘은 우선순위 큐 없이, 서로소 집합(유니온 파인드)으로 구현되고 아래 동작으로 정의된다.
-
임의의 시작 정점을 선택하여 트리에 포함시킨다.
-
선택된 정점과 연결된 간선 중에서 가장 가중치가 작은 간선을 선택하여 트리에 포함시킨다.
-
트리에 포함된 정점들과 외부의 정점들을 연결하는 간선 중에서 가장 가중치가 작은 간선을 선택하여 트리에 포함시킨다.
-
위의 과정을 트리가 모든 정점을 포함할 때까지 반복한다.
하지만, 위의 과정은 직관적이지 않다.
그래서 작동 과정을 그림으로 준비했다.
일단 dist 배열과 union-find 구조의 parent 배열을 준비한다.
parent는 평범한 유니온 파인드처럼 처음에 각각 자신을 가리키게 한다.
그리고 dist는 i번 정점이 초기 스패닝 트리와 연결되어 있다면 그중 가장 작은 가중치를, 이미 트리에 속했다면 0, 트리와 연결되어 있지 않다면 INF로 초기화한다.
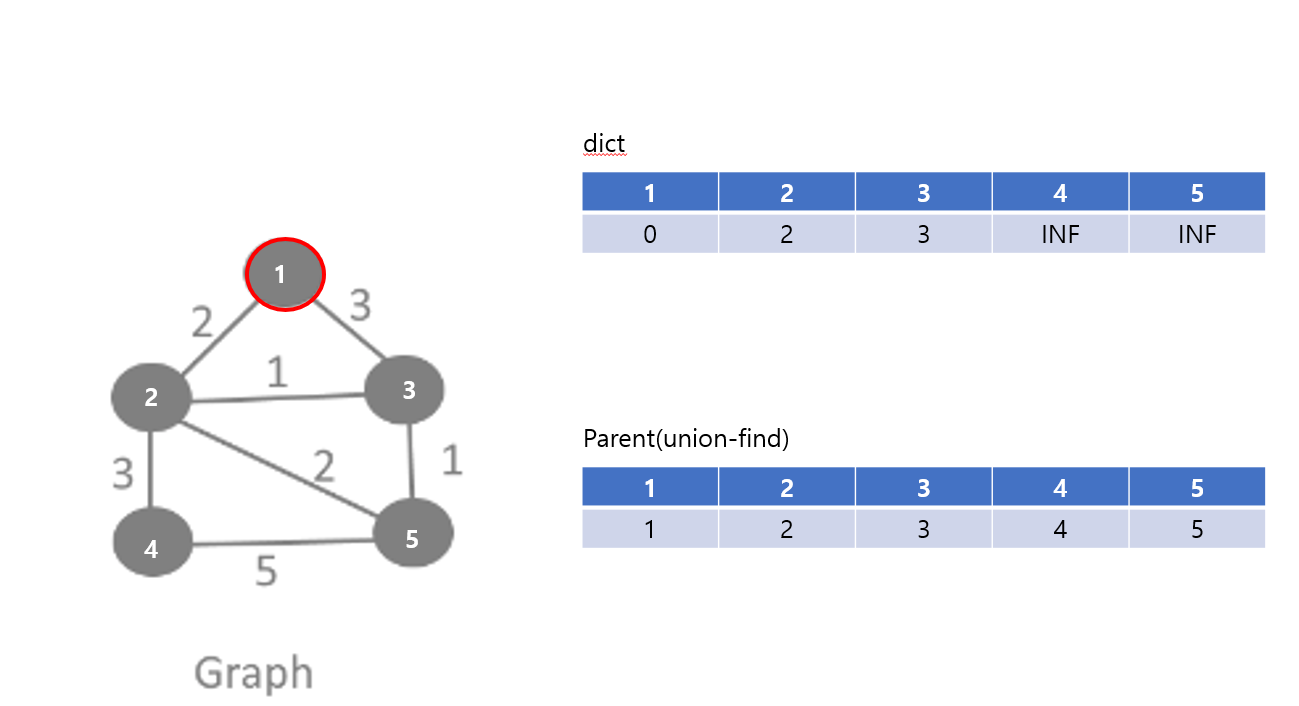
그 후, 트리와 연결된 정점 중 가중치가 더 작은 2번 노드를 연결한다.
union-find 배열을 갱신한다.
또, 2번이 트리에 연결됐으니 dist 배열의 값을 갱신해줘야 한다.
2번은 이제 트리에 속하게 됐으니 0으로 갱신한다.
그리고 3번은 트리의 노드 중 1번보다 2번과 더 가까우니 그 가중치 1로 갱신한다.
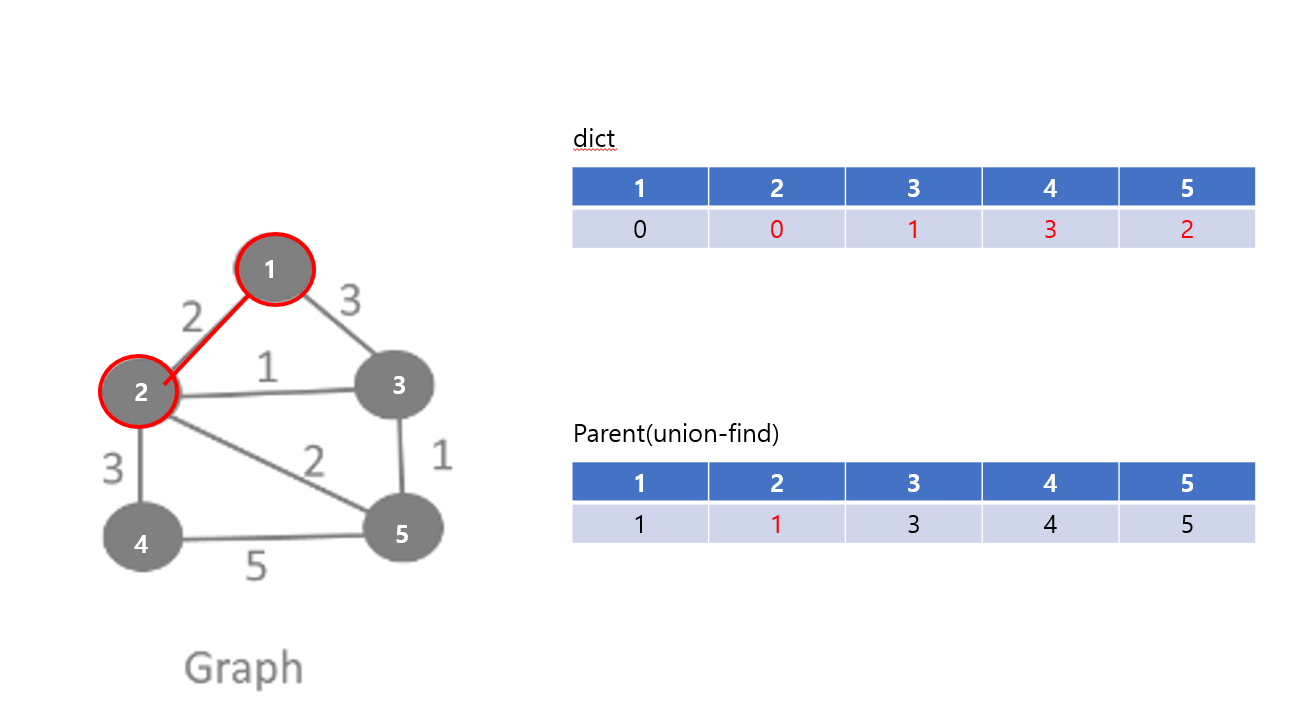
똑같은 작업으로, 3번, 4번, 5번 노드 중 가장 가중치가 작은 3번과 연결한다.
또, 두 배열을 갱신한다.
3번을 연결하게 되면, 5번은 트리의 노드 중 1, 2, 3 중 3번과 가장 가까우니 그 가중치인 1로 업데이트된다.

위와 같이 반복한다.
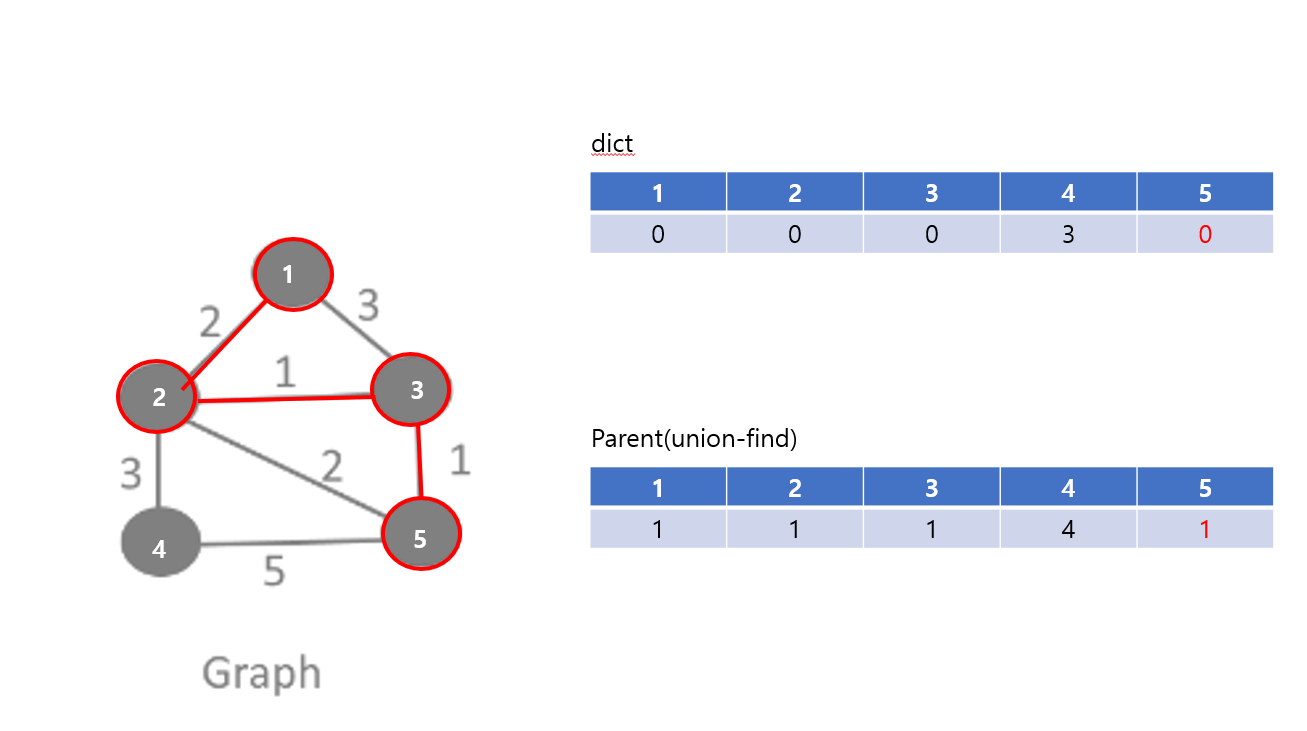
마지막 정점인 5번을 추가하면 최소 스패닝 트리가 만들어진다.
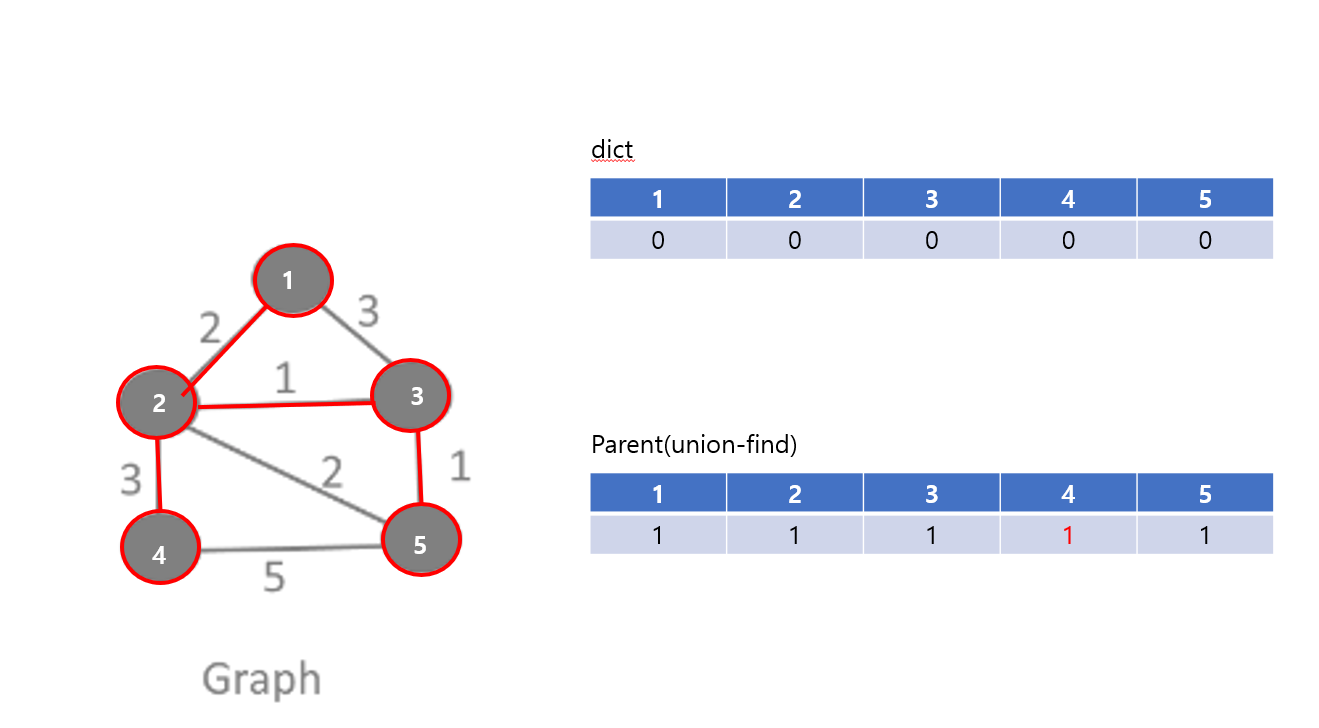
프림 알고리즘의 구현
조금 복잡해서 실제 구현 코드는 아니지만, 대충의 틀을 보여주기 위해 코드를 작성했다.
아래와 같이 실제 프로그래밍 언어의 문법이나 규칙을 따르지 않고, 인간이 이해하기 쉽게 표현된 코드를 의사 코드(pseudo-code)라고도 한다.
int primMST(struct EdgeInfo edges[], int numEdges, int startVertex) {
// 유니온-파인드를 위한 배열 초기화
int parent[NODE + 1];
for (int i = 1; i <= NODE; i++) {
parent[i] = i;
}
int num_of_tree_node = 1;
// 스패닝 트리에 포함된 정점 수
//임의의 시작 정점을 선택하여 트리에 포함시킨다.
int total_cost = 0;
// 총 가중치 합
// 시작 정점을 스패닝 트리에 추가
// 여기서는 간선이 없는 정점으로 가정
// 실제 구현에서는 dist 배열 초기화 등이 필요할 수 있음
// 스패닝 트리를 만들 때까지 반복
while (numTreeNodes < NODE) {
// 아직 트리에 속하지 않은 정점 중에서 가장 작은 간선 선택 및 추가
// 유니온-파인드 연산을 통해 정점을 스패닝 트리에 추가
// 스패닝 트리에 포함된 정점 수 증가
// 선택한 간선의 가중치를 총 가중치 합에 추가
// 선택한 정점을 기준으로 다른 정점들과의 거리 업데이트
}
return totalCost;
}
위 코드에 순서대로 구현을 채워 넣으면 된다.
조금 복잡할 수 있는데, 역시 최대한 구현해보다가 답을 보도록 하자.
#include <stdio.h>
#include <stdlib.h>
#include "Union_find.h"
#define INF 123456789
typedef struct input {
int vertex1;
int vertex2;
int weight;
}info;
int is_tree(int parent[], const int target, const int start) {
if (find(parent, target) == find(parent, start)) {
return 1;
}
else {
return 0;
}
}
void make_matrix(info info_arr[], int matrix[][NODE + 1], const int parent_num) {
for (int i = 0; i < parent_num; i++) {
int v1 = info_arr[i].vertex1;
int v2 = info_arr[i].vertex2;
int w = info_arr[i].weight;
matrix[v1][v2] = w;
matrix[v2][v1] = w;
}
}
void init_dist(int matrix[][NODE + 1], int dist[], const int start) {
for (int i = 1; i <= NODE; i++) {
if (start == i) {
dist[i] = 0;
// 이미 트리라면 0
}
else if (matrix[start][i] != 0) {
dist[i] = matrix[start][i];
// 스패닝 트리와 연결되지 않는다면 INF
}
}
}
void update(int matrix[][NODE + 1], int dist[], const int target_v) {
for (int i = 1; i <= NODE; i++) {
if (target_v == i) {
dist[i] = 0;
// 이미 트리라면 0
}
else if (matrix[target_v][i] != 0) {
if (dist[i] > matrix[target_v][i]) {
dist[i] = matrix[target_v][i];
}
// 새로 추가된 target_v를 통해 연결할 수 있고
// 기존의 dist보다 작은 값을 가진다면 바꿈
}
}
}
int Prim(info info_arr[], const int parent_num, const int start) {
int matrix[NODE + 1][NODE + 1] = { 0, };
make_matrix(info_arr, matrix, parent_num);
//쉬운 처리를 위해 인접행렬 사용
int parent[NODE + 1] = { 0 , };
init(parent);
// 유니온-파인드를 위한 배열 초기화
int num_of_tree_node = 1;
// 스패닝 트리에 포함된 정점 수
//임의의 시작 정점을 선택하여 트리에 포함시킨다.
int total_cost = 0;
// 총 가중치 합
int dist[6] = {INF, INF, INF, INF, INF, INF };
// 스패닝 트리가 아닌 원소와 이미 트리인 원소의 사이 간선 중
// 가중치가 가장 작은 간선의 가중치
init_dist(matrix, dist, start);
// dist 배열 초기화
// 스패닝 트리를 만들 때까지 반복
while (num_of_tree_node < NODE) {
int target_v;
int min = INF;// 초기화
for (int i = 1; i <= NODE; i++) {
if (!is_tree(parent, i, start)) {
if (min > dist[i]) {
min = dist[i];
target_v = i;
}
}
}
// 아직 트리에 속하지 않은 정점 중에서
// 가장 작은 간선을 가진 정점 선택
_union(parent, target_v, start);
// 유니온-파인드 연산을 통해 정점을 스패닝 트리에 추가
num_of_tree_node += 1;
// 스패닝 트리에 포함된 정점 수 증가
total_cost += min;
// 선택한 간선의 가중치를 총 가중치 합에 추가
// dist 최신화
update(matrix, dist, target_v);
}
// 선택한 정점을 기준으로 다른 정점들과의 거리 업데이트
return total_cost;
}
int main(void) {
info parent[] = { {1, 2, 2}, {1, 3, 3}, {2, 3, 1}, {2, 4, 3}, {2, 5, 2}, {4, 5, 5}, {3, 5, 1} };
// 정점 연결, 가중치 정보
int parent_num = sizeof(parent) / sizeof(info);
printf("The minimum cost of spanning tree is %d", Prim(parent, parent_num, 1));
// 임의의 정점 1에서 시작
}
✅ 1. 최소 스패닝 트리(Minimum Spanning Tree)의 뜻을 안다.
✅ 2. 크루스칼 알고리즘을 통해서 최소 스패닝 트리를 구할 수 있다.
✅ 3. 프림 알고리즘을 통해서 최소 스패닝 트리를 구할 수 있다.
⚠️ 최소 스패닝 트리를 MST라고도 한다.
💣 과제,
- 인접 리스트를 통해서 프림 알고리즘도 구현해보자(난이도 中)
🔜 더 공부해보기,



Comments